 Hypotheses
Experiment
Hypotheses
Experiment
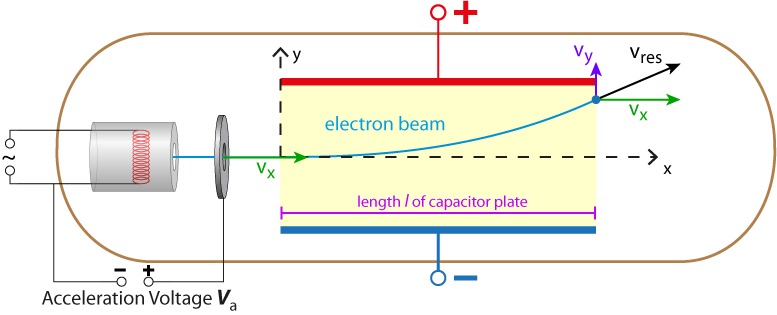
| equation of motion in y-direction |
|---|
| $$\begin{equation}y(t)=\frac{1}{2}a_y\cdot t^2\end{equation}$$ |
| $$\begin{equation}v_y(t)=a_y\cdot t\end{equation}$$ |
| $$\begin{equation}a_y(t)=\frac{F}{m}=\frac{V_{\text p}\cdot e}{m\cdot \text{d}}\end{equation}$$ |