Experimental validation of the de Broglie Theory

With the help of an elctron diffraction tube, we will experimentally validate that de Broglie's assumption is true and material particles do indeed posess wavelength $\lambda_{\text{de Broglie}} =\frac {h}{m_\text e\cdot v_\text e}$.
In order to do so we must demonstrate using this Experiment that the circular rings are indeed interference maxima resulting from electrons undergoing diffraction from the graphite film.
Interference maxima arise when the Bragg condition $$\begin{equation}\text n\cdot \lambda=2\cdot d\cdot \sin(\theta)\end{equation}$$is fulfilled.

Tube geometry

Furthermore, the geometry of the tube plays a roll.Let \(L=\) distance from graphite to screen, \(R=\) radius of the glass sphere, and \(r=\) radius of the rings on the screen.

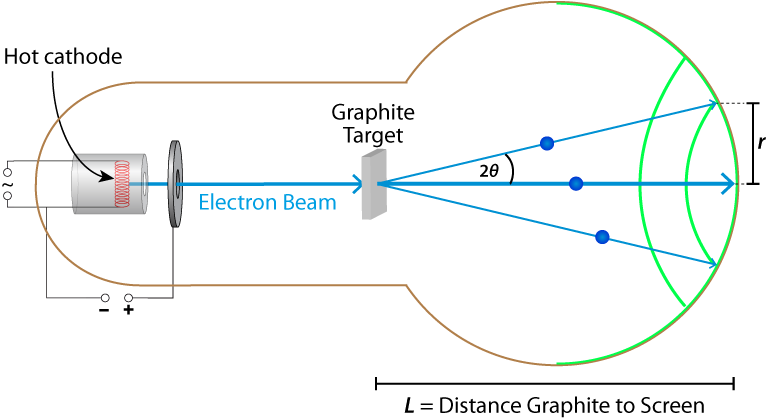
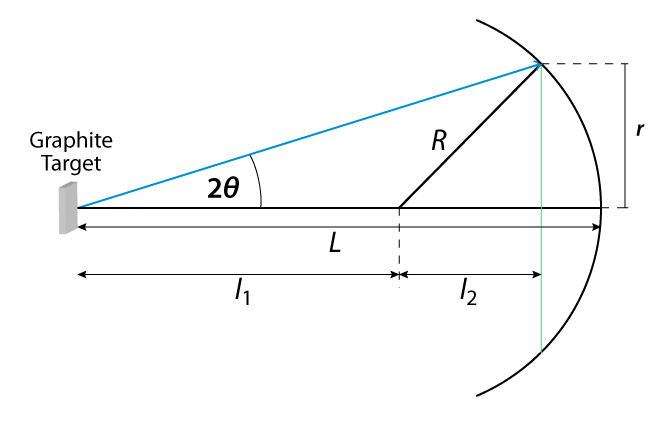
The angle $\theta$ is described by the following relation: $$\begin{equation}\tan(2\,\theta)=\frac{r}{l_1+l_2}\end{equation}$$From $l_1=L-R$ and $l_2=\sqrt{R^2-r^2}$ follows: $$\begin{equation}\tan(2\,\theta)=\frac{r}{L-R+\sqrt{R^2-r^2}}\quad\Rightarrow\quad\theta=\frac{1}{2}\cdot \tan^{-1}\left(\frac{r}{L-R+\sqrt{R^2-r^2}}\right)\end{equation}$$ Substitution into the Bragg condition (1) shows that the inner ring is the first order diffraction maximum where n=1, and the wavelength $\lambda$ $$\begin{equation}\bbox[8px,border:2px solid red]{\lambda=2\cdot d\cdot \sin\left(\frac{1}{2}\cdot \tan^{-1}\left(\frac{r}{L-R+\sqrt{R^2-r^2}}\right)\right)}\end{equation}$$follows, where $d=2{.}13\cdot 10^{-10}\,\text m$ is the lattice spacing of graphite. The dimensions \(L\) und \(R\) are particular to the tube and can be measured. For the tube used here, \(L=12.7\,\rm{cm}\) and \(R=6.35\,\rm{cm}\).

To be tested in experiment

The experiment shows that the (4) calculated wavelength $\lambda_{\text{de Broglie}} =\frac {h}{m_\text e\cdot v_\text e}$ is indeed the de Broglie wavelengths.

next