 Introduction
Wavelength
Diffraction
Introduction
Wavelength
DiffractionOrder Graphite Grating Tasks
In the experiment we see on the screen a second, outer ring with a larger radius. The second ring appears similair to the inner diffraction ring. If the acceleration voltage of the electron gun is increased, the radius of both rings are reduced. One could say that the second ring is a second order interference maximum. In the case of diffraction of light from multiple slits, it is easy to recognize the interference maxima of higher orders:
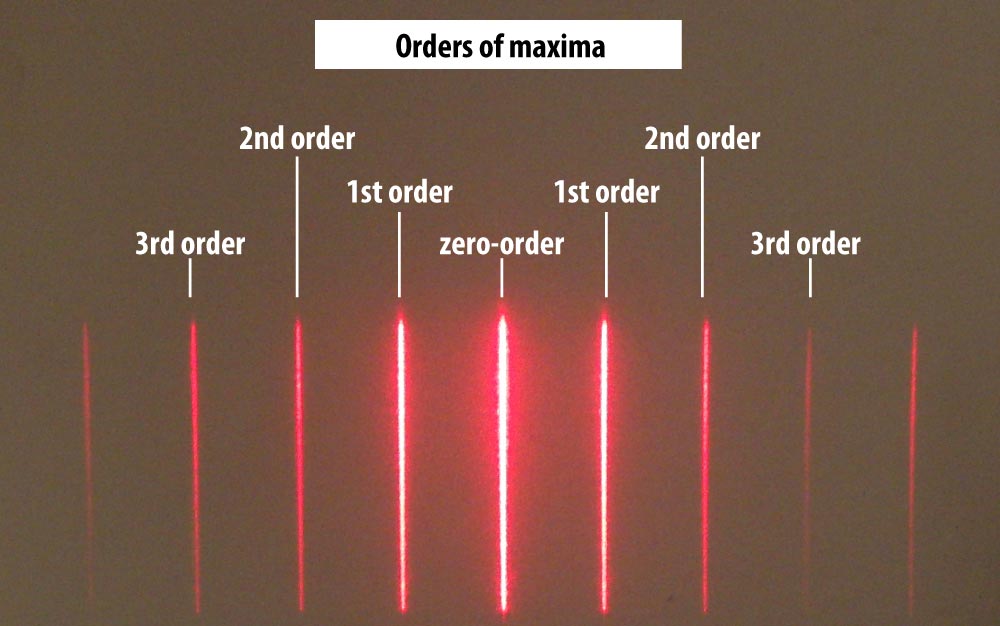
In the case of electron diffraction, such a second order maximum would have to satisfy the Bragg condition for \(n=2\): $$2\cdot \lambda = 2\cdot d\cdot \sin(\theta)\quad\Rightarrow\quad \lambda = d\cdot \sin(\theta)$$ Using the formula derived from the tube geometry for θ yields $$\lambda =d\cdot \sin\left(\frac{1}{2}\tan^{-1}\left(\frac{r}{L-R+\sqrt{R^2-r^2}}\right)\right)$$ If the second ring is the second order interference maximum, then this wavelength must again be the de Broglie wavelength $\lambda_{\text {de Broglie}}= \frac{h}{p_{\text e}}$.