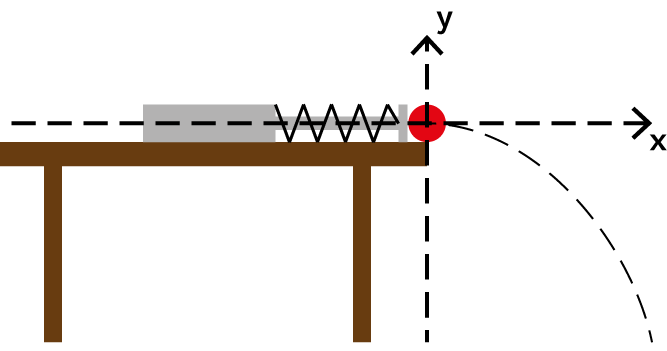
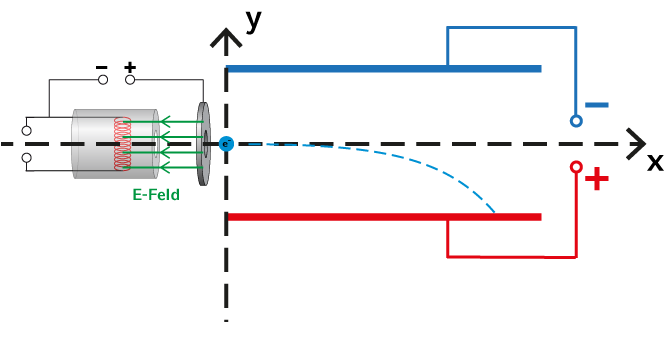
To describe the trajectory in only one equation we have to solve the equitaion of the motion in x-direction$$\begin{equation}x(t)= v_0\cdot t\end{equation}$$ for t and plug in the equation of the motion in y-direction $$\begin{equation}y(t)=\frac{1}{2}a_y\cdot t^2\end{equation}$$ This yields the searched equation: $$\begin{equation}y(x)= \frac{1}{2}\cdot a_y \cdot \frac{x^2}{{v_0}^2}.\end{equation}$$ If plugging g for the acceleration in y-direction, it shows $$\begin{equation}y(x)= -\frac{1}{2}\cdot g \cdot \frac{x^2}{{v_0}^2}.\end{equation}$$ With the equation for $v_0$ determined here, it yields$$\begin{equation}y(x)= -\frac{1}{2}\cdot \frac{g\cdot m}{D\cdot s^2}\cdot x^2.\end{equation}$$
$v_0=$ initial speed in x-direction,
$g=$ gravitational acceleration,
$D=$ Stiffness of the spring,
$s=$ Extension,
$m=$ Mass of the sphere

Here also the equations for the motions in x- ans y-direction must be plugged in each other. There we solve the equation$$\begin{equation}x(t)= v_0\cdot t\end{equation}$$ for t and plug it in$$\begin{equation}y(t)=\frac{1}{2}a_y\cdot t^2\end{equation}$$ This yields the searched equation:$$\begin{equation}y(x)= \frac{1}{2}\cdot a_y \cdot \frac{x^2}{{v_0}^2}.\end{equation}$$ Here $a_y$ can be replaced by the acceleration of the electrons in the electric field:$$\begin{equation}y(x)= -\frac{1}{2}\cdot \frac{V_{\text p}\cdot e}{\text{d}\cdot m_e \cdot{v_0}^2}\cdot x^2.\end{equation}$$ With the equation for $v_0$ determined here, it yields:$$\begin{equation}y(x)= -\frac{1}{4\cdot \text{d}}\cdot \frac{V_{\text p}}{V_{\text a}}\cdot x^2.\end{equation}$$
$v_0=$ initial speed in horizontal direction,
$V_{\text{p}}=$ potential between capacitor plates,
$V_{\text{a}}=$ acceleration voltage,
d = distance between capacitor plates,
$e=$ Elementary charge,
$m_e=$ Mass of an electron