DEBYE-SCHERRER-Streuung aus Abi 2010 in BY

(Quelle: ISB)


Aufgabe

Materiewellen wurden 1924 postuliert und kurze Zeit später mit Versuchen wie dem DEBYE-SCHERRER-Verfahren nachgewiesen. In einer Vakuumröhre treffen Elektronen, die aus einem Glühdraht (Heizspannung ${U_{\rm{H}}}$) ausgetreten sind und durch die Spannung ${U_{\rm{B}}}$ beschleunigt wurden, auf ein Pulver aus Graphitkristallen. Dahinter werden sie auf einem Leuchtschirm sichtbar gemacht. Typischerweise beobachtet man um einen hellen Mittelpunkt konzentrische, helle Kreisringe.
  1. Leite anhand geeigneter Skizzen den Zusammenhang zwischen der Wellenlänge einer auftreffenden Welle und ihren möglichen Ablenkwinkeln bei der Beugung am Einkristall her (BRAGG-Bedingung).
    Erkläre damit das Zustandekommen des beobachteten Bildes.

  2. Erläutere, wie man experimentell nachweisen kann, dass die gezeigten Erscheinungen tatsächlich von Elektronen erzeugt werden und nicht von Röntgenstrahlung, die beim Auftreffen von Elektronen auf das Pulver entstanden sein könnte.
    Bei den konzentrischen Kreisen handelt es sich um Beugungen an zwei verschiedenen Netzebenen des Graphits mit den Netzebenenabständen ${d_1} = 1{,}23 \cdot {10^{ - 10}}{\rm{m}}$ und ${d_2} = 2{,}13 \cdot {10^{ - 10}}\,{\rm{m}}$. Der kreisförmige Leuchtschirm (Radius $R = 4{,}7\,{\rm{cm}}$) hat von der Graphitpulverschicht den Abstand $L = 13{,}5\,{\rm{cm}}$. Die Beschleunigungsspannung ${U_{\rm{B}}}$ ist auf $4{,}0\,{\rm{kV}}$ eingestellt.

  3. Berechne relativistisch die de BROGLIE-Wellenlänge $\lambda $ eines anfangs ruhenden Elektrons, welches die Beschleunigungsspannung ${U_{\rm{B}}}$ durchlaufen hat. [zur Kontrolle: $\lambda  = 1{,}9 \cdot {10^{ - 11}}{\rm{m}}$]

  4. Bestimme, wie viele Kreise bei diesem Versuch theoretisch auf dem Leuchtschirm zu erwarten sind.

  5. Beschreibe und erkläre, wie sich das Bild auf dem Schirm verändert, wenn man zum einen die Spannung ${U_{\rm{H}}}$ bzw. zum anderen die Spannung ${U_{\rm{B}}}$ vergrößert.

  6. Zeige für den Fall kleiner Beschleunigungsspannungen (nichtrelativistischer Ansatz), dass für den Zusammenhang zwischen der Beschleunigungsspannung ${U_{\rm{B}}}$ und der de BROGLIE-Wellenlänge $\lambda $ gilt: $$U_{\rm{B}} = \frac{h^2}{2\cdot e \cdot m \cdot \lambda^2}$$
    Bestimme damit die kleinstmöglich Beschleunigungsspannung ${U_{\rm{B}}}$, ab der theoretisch überhaupt Interferenzkreise auf dem Leuchtschirm zu erwarten sind.

Lösungen:

 
  1. Für den Gangunterschied zwischen den beiden an der oberen und an der darunter liegenden Netzebene gilt \[{\Delta s = \overline {AB}  + \overline {BC}  = 2 \cdot d \cdot \sin \left( \theta \right)}\] Konstruktive Interferenz tritt auf, wenn \[k \cdot \lambda  = 2 \cdot d \cdot \sin \left( \theta  \right)\;,\;k \in \mathbb{N}\] was üblicherweise als BRAGG-Beziehung bezeichnet wird. Der Winkel \(\theta \) kann mathematisch exakt aus der Beziehung \[\tan(2 \theta)= \frac{r}{l_1+l_2}\]ermittelt werden.
    Häufig wird jedoch auch als einfache Näherung \[\tan \left( {2 \theta } \right) = \frac{r}{L}\] genutzt, da der Abstand zwischen dem Graphitblättchen und der Glasröhre im Datenblatt angegeben ist.

    Im Graphitpulver liegen nun stets einige Kristallite so, dass sie unter dem Glanzwinkel \(\theta \) getroffen werden. Auf diese Weise kommt es zu einem „Strahlungskegel“, dessen Spitze im Graphitpulver liegt und dessen Grundkreis die Glaskugel schneidet.

  2. Ein Magnet zwischen Kristallpulver und Leuchtschirm verändert das Bild auf dem Schirm. Röntgenstrahlen würden vom Magneten nicht beeinflusst.

  3. Für die Gesamtenergie \(E\) der Elektronen gilt \[E = {E_0} + {E_{{\rm{kin}}}} = {E_0} + e \cdot {U_{\rm{B}}}\] Den Impuls der Elektronen erhält man über die relativistische Energie-Impuls-Beziehung \[{{E^2} = E_0^2 + {p^2} \cdot {c^2} \Rightarrow p = \frac{1}{c} \cdot \sqrt {{E^2} - E_0^2} }\] Einsetzen der gegebenen Werte liefert \[{p=\frac{1}{{3{,}0 \cdot {{10}^8}\frac{{\rm{m}}}{{\rm{s}}}}} \cdot \sqrt {{{\left( {\left( {511 \cdot {{10}^3}{\rm{eV}}+4{,}0 \cdot {{10}^3}{\rm{eV}}} \right) \cdot 1{,}60 \cdot {{10}^{-19}}} \right)}^2}-{{\left( {511 \cdot {{10}^3}{\rm{eV}} \cdot 1{,}60 \cdot {{10}^{-19}}} \right)}^2}}=3{,}4 \cdot {{10}^{-23}}{\rm{Ns}}}\] Mit Hilfe der de BROGLIE-Beziehung erhält man für die Wellenlänge \[\lambda  = \frac{h}{p} \Rightarrow \lambda  = \frac{{6{,}63 \cdot {{10}^{ - 34}}{\rm{Js}}}}{{3{,}42 \cdot {{10}^{ - 23}}{\rm{Ns}}}} = 1{,}94 \cdot {10^{ - 11}}{\rm{m}}\]

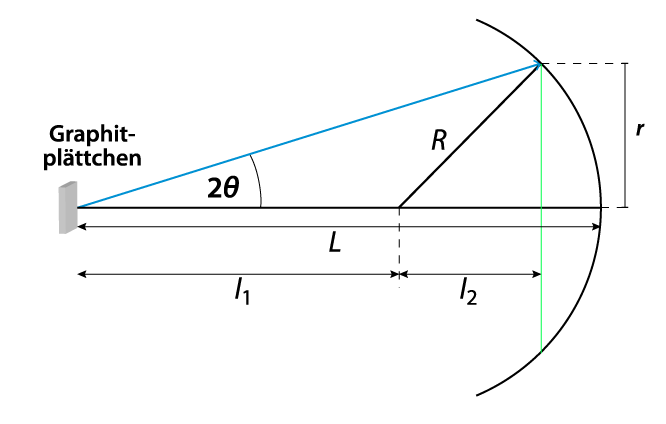
  4. Die obere Grenze für den Radius eines Interferenzringes ist der Radius des Leuchtschirms \(R = 4{,}7{\rm{cm}}\). Zur Bestimmung des Winkels \(\theta\) muss die Näherung aus Teilaufgabe b) verwendet werden, da nur die Röhrenlänge bekannt ist.
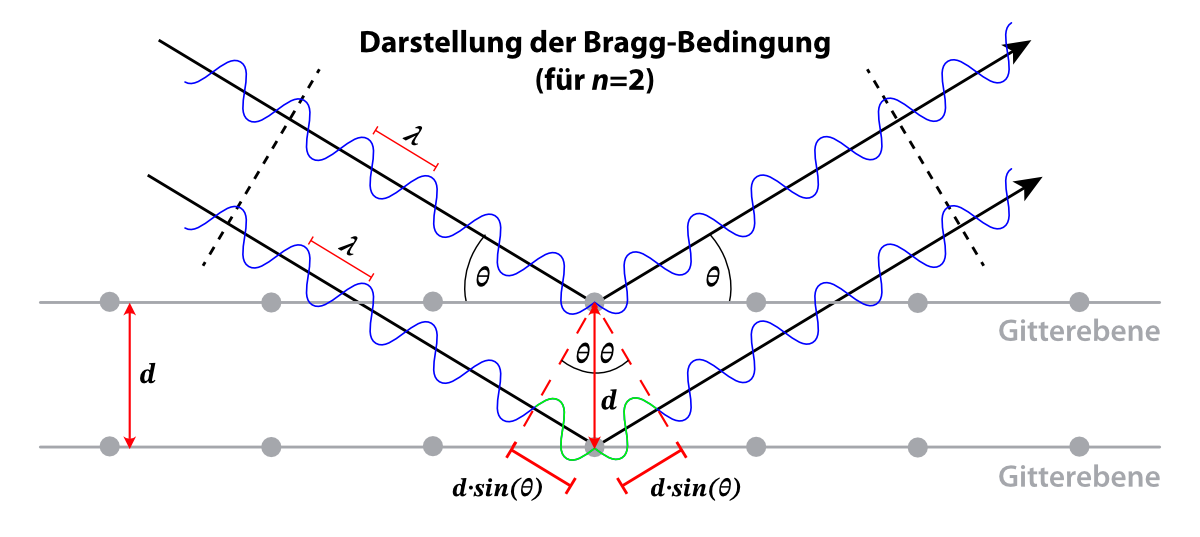
    Somit gilt für \({{\theta _{\max }}}\) \[{\tan \left( {2 \cdot {\theta _{\max }}} \right) \le \frac{R}{L} \Rightarrow \tan \left( {2 \cdot {\theta _{\max }}} \right) \le \frac{{4{,}7}}{{13{,}5}} = 0{,}35 \Rightarrow {\theta _{\max }} \le 9{,}6^\circ }\] Mit Hilfe der BRAGG-Beziehung erhält man die Zahl der möglichen Ringe. Für \({d_1} = 1{,}23 \cdot {10^{ - 10}}{\rm{m}}\) ergibt sich \[{k_1} \cdot \lambda  \le 2 \cdot {d_1} \cdot \sin \left( {{\theta _{\max }}} \right) \Leftrightarrow {k_1} \le \frac{{2 \cdot {d_1} \cdot \sin \left( {{\theta _{\max }}} \right)}}{\lambda } \Rightarrow {k_1} \le \frac{{2 \cdot 1{,}23 \cdot {{10}^{ - 10}}{\rm{m}} \cdot \sin \left( {9{,}6^\circ } \right)}}{{1{,}94 \cdot {{10}^{ - 11}}{\rm{m}}}} \Rightarrow {k_1} \le 2{,}2\] und analog für \({d_2} = 2{,}13 \cdot {10^{ - 10}}{\rm{m}}\) \[{k_2} \le \frac{{2 \cdot 2{,}13 \cdot {{10}^{ - 10}}{\rm{m}} \cdot \sin \left( {9{,}6^\circ } \right)}}{{1{,}94 \cdot {{10}^{ - 11}}{\rm{m}}}} \Rightarrow {k_2} \le 3{,}7\] Da \(k \in \mathbb{N}\) gilt, folgt: es gibt 2 Ringe + 3 Ringe = 5 Ringe

  5. Bei Vergrößerung der Heizspannung \({U_{\rm{H}}}\) treten mehr Elektronen pro Zeiteinheit aus dem Glühdraht. Dadurch wird das Bild der Interferenzringe intensiver.

    Bei Vergrößerung der Beschleunigungsspannung \({U_{\rm{B}}}\) nimmt die Elektronengeschwindigkeit zu und die de BROGLIE-Wellenlänge wird kleiner. Aus der BRAGG-Beziehung ersieht man, dass dann der Glanzwinkel \(\theta \) kleiner wird und sich somit der Radius der Ringe verkleinert.

  6. Der nichtrelativistische Ansatz für die kinetische Energie ergibt \[{e \cdot {U_{\rm{B}}} = {E_{{\rm{kin}}}} = \frac{1}{2} \cdot m \cdot {v^2} \Leftrightarrow {U_B} = \frac{{m \cdot {v^2}}}{{2 \cdot e}}\quad(1)}\] die de BROGLIE-Beziehung liefert \[{m \cdot v = p = \frac{h}{\lambda } \Leftrightarrow v = \frac{h}{{m \cdot \lambda }}\quad(2)}\] Einsetzen von \((2)\) in \((1)\) liefert \[{{U_{\rm{B}}} = \frac{{{h^2}}}{{2 \cdot e \cdot m \cdot {\lambda ^2}}}}\] Obige Beziehung besagt, dass die Beschleunigungsspannung am kleinsten ausfällt, wenn die Materiewellenlänge am größten ist.

    Aus der BRAGG-Beziehung \[k \cdot \lambda  = 2 \cdot d \cdot \sin \left( \theta  \right) \Leftrightarrow \lambda  = \frac{{2 \cdot d \cdot \sin \left( \theta  \right)}}{k}\] erkennt man, dass \(\lambda \) am größten ist, wenn \(k\) möglichst klein, also \(k = 1\), \(d\) möglichst groß, also \(d = d_2\)) und \(\theta \) maximal ist, also \({\theta  = {\theta _{\max }}}\). Damit ergibt sich \[{\lambda _{\max }} = \frac{{2 \cdot 2{,}13 \cdot {{10}^{ - 10}}{\rm{m}} \cdot \sin \left( {{{9{,}6}^\circ }} \right)}}{1} = 7{,}1 \cdot {10^{ - 11}}\,{\rm{m}}\]
    Für \({U_{\rm{B}}}\) ergibt sich dann \[{U_{\rm{B}}} = \frac{{{h^2}}}{{2 \cdot e \cdot m \cdot {\lambda ^2}}} \Rightarrow {U_{\rm{B}}} = \frac{{{{\left( {6{,}63 \cdot {{10}^{ - 34}}{\rm{Js}}} \right)}^2}}}{{2 \cdot 1{,}60 \cdot {{10}^{ - 19}}{\rm{As}} \cdot 9{,}11 \cdot {{10}^{ - 31}}{\rm{kg}} \cdot {{\left( {7{,}1 \cdot {{10}^{ - 11}}{\rm{m}}} \right)}^2}}} = 3{,}0 \cdot {10^2}\,{\rm{V}} = 0{,}30\,{\rm{kV}}\]