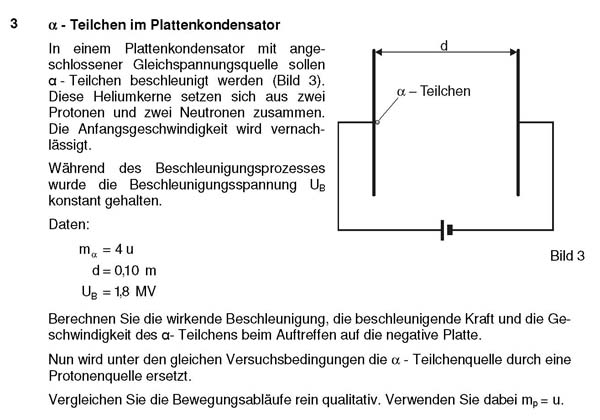
Aufgabe 2: Alpha-Teilchen im Plattenkondensator aus Abi 2012 in Sachsen
Lösung:
Die beschleunigende Kraft ist die elektrische Kraft $F_{\text {el}}$ auf das Teilchen im Plattenkondensator mit dem Plattenabstand d:
$$F_{\text {el}}=E\cdot q = \frac {U\cdot q}{\text d}\Rightarrow F_{\text {el}}=\frac{1{,}8\cdot 10^6\,\text V \cdot 2\cdot 1{,}6\cdot 10^{-19}\,\text C}{0{,}1\,\text m}=5{,}76\cdot 10^{-12}\,\text N $$
Es handelt sich hier um eine konstant beschleunigte Bewegung, daher gilt:
$$F= m\cdot a \Rightarrow a = \frac{F}{m}$$
Einsetzen liefert:
$$a=\frac{U\cdot q}{\text{d}\cdot m} \Rightarrow a = \frac{1{,}8\cdot 10^6\,\text{V}\cdot 2\cdot 1{,}6\cdot 10^{-19}\,\text {C}} {0{,}1\,\text{m}\cdot 4 \cdot 1{,}66\cdot 10^{-27}\,\text{kg}}\approx 8{,}67\cdot 10^{14}\,\frac{\text m}{\text {s}^2}$$
Die kinetische Energie der α-Teilchen ist gleich der vom elektrische Feld verrichten Beschleunigungsarbeit:
$$\frac{1}{2} \cdot m \cdot v^2 = q \cdot U \Rightarrow v = \sqrt{\frac{2 \cdot q \cdot U}{m}} $$
$$v = \sqrt{\frac{2\cdot 2\cdot 1{,}6 \cdot 10^{-19}\,\text{C} \cdot 1{,}8\cdot 10^6 \,\text V}{4 \cdot 1{,}66\cdot 10^{-27}\,\text{kg}}} \approx 1{,}317 \cdot 10^7\, \frac{\text m}{\text s}$$
Ein einzelnes Proton hat nur ein Viertel der Masse m und die Hälfte der Ladung q im Vergleich zum α-Teilchen.
Daher wirkt im E-Feld auf das Proton zwar nur die Hälfte der Kraft im Vergleich mit dem α-Teilchen, aber da es nur 1/4 soviel wiegt, ist die Beschleunigung des Protons doppelt so groß, wie die des α-Teilchen.
Bezüglich der Geschwindigkeit beim Auftreffen auf die Platte kommt noch die Wurzel zum Tragen. Diese erhöht sich also um den Faktor $\sqrt{2}$.
Ansonsten handelt es sich bei beiden Bewegungen um konstant beschleunigte Bewegungen und beide Teilchen bewegen sich von der positiv zur negativ geladenen Platte hin.
 Hypothesen
Experiment
Kräfte-
Hypothesen
Experiment
Kräfte-