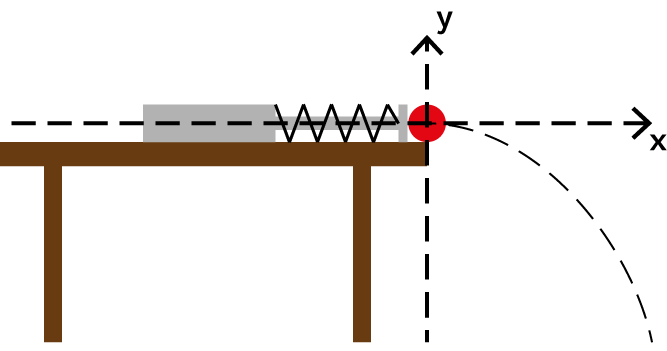
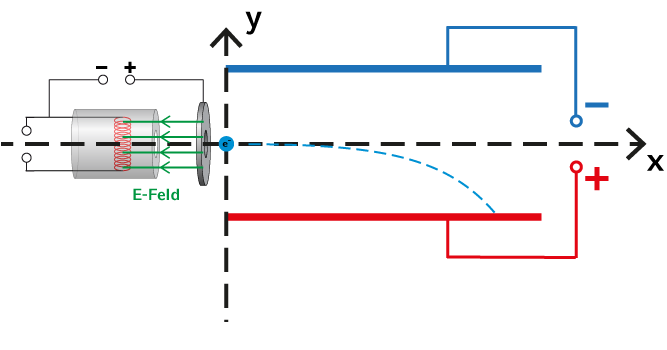
Um die Flugbahn mit einer einzigen Gleichung beschreiben zu können, muss man die Bewegungsgleichung in x-Richtung$$\begin{equation}x(t)= v_0\cdot t\end{equation}$$ nach t auflösen und in die Bewegungsgleichung der y-Richtung $$\begin{equation}y(t)=\frac{1}{2}a_y\cdot t^2\end{equation}$$ einsetzen. Dies liefert die gesuchte Funktionsgleichung: $$\begin{equation}y(x)= \frac{1}{2}\cdot a_y \cdot \frac{x^2}{{v_0}^2}.\end{equation}$$ Setzt man für die Beschleunigung in y- Richtung noch g ein, erhält man $$\begin{equation}y(x)= -\frac{1}{2}\cdot g \cdot \frac{x^2}{{v_0}^2}.\end{equation}$$ Mithilfe des hier ermittelten Ausdrucks für $v_0$ kommt man zu$$\begin{equation}y(x)= -\frac{1}{2}\cdot \frac{g\cdot m}{D\cdot s^2}\cdot x^2.\end{equation}$$
$v_0=$ Anfangsgeschwindigkeit in x-Richtung,
$g=$ Erdbeschleunigung,
$D=$ Federkonstante,
$s=$ Federweg,
$m=$ Masse der Kugel

Auch hier muss man die Bewegungsgleichungen der x- und y- Richtung ineinander einsetzen. Dazu löst man die Gleichung$$\begin{equation}x(t)= v_0\cdot t\end{equation}$$ nach t auf und setzt sie in$$\begin{equation}y(t)=\frac{1}{2}a_y\cdot t^2\end{equation}$$ ein. Dies liefert die gesuchte Funktionsgleichung:$$\begin{equation}y(x)= \frac{1}{2}\cdot a_y \cdot \frac{x^2}{{v_0}^2}.\end{equation}$$ Hier kann $a_y$ noch durch die Beschleunigung des Elektrons im E-Feld ersetzt werden:$$\begin{equation}y(x)= -\frac{1}{2}\cdot \frac{U_{\text p}\cdot e}{\text{d}\cdot m_e \cdot{v_0}^2}\cdot x^2.\end{equation}$$ Mit dem hier ermittelten Ausdruck für $v_0$ erhält man durch einsetzen und kürzen:$$\begin{equation}y(x)= -\frac{1}{4\cdot \text{d}}\cdot \frac{U_{\text p}}{U_{\text b}}\cdot x^2.\end{equation}$$
$v_0=$ Anfangsgeschwindigkeit in x-Richtung,
$U_{\text{p}}=$ Plattenspannung,
$U_{\text{b}}=$ Beschleunigungsspannung,
d = Abstand der Kondensatorplatten,
$e=$ Elementarladung,
$m_e=$ Masse eines Elektrons